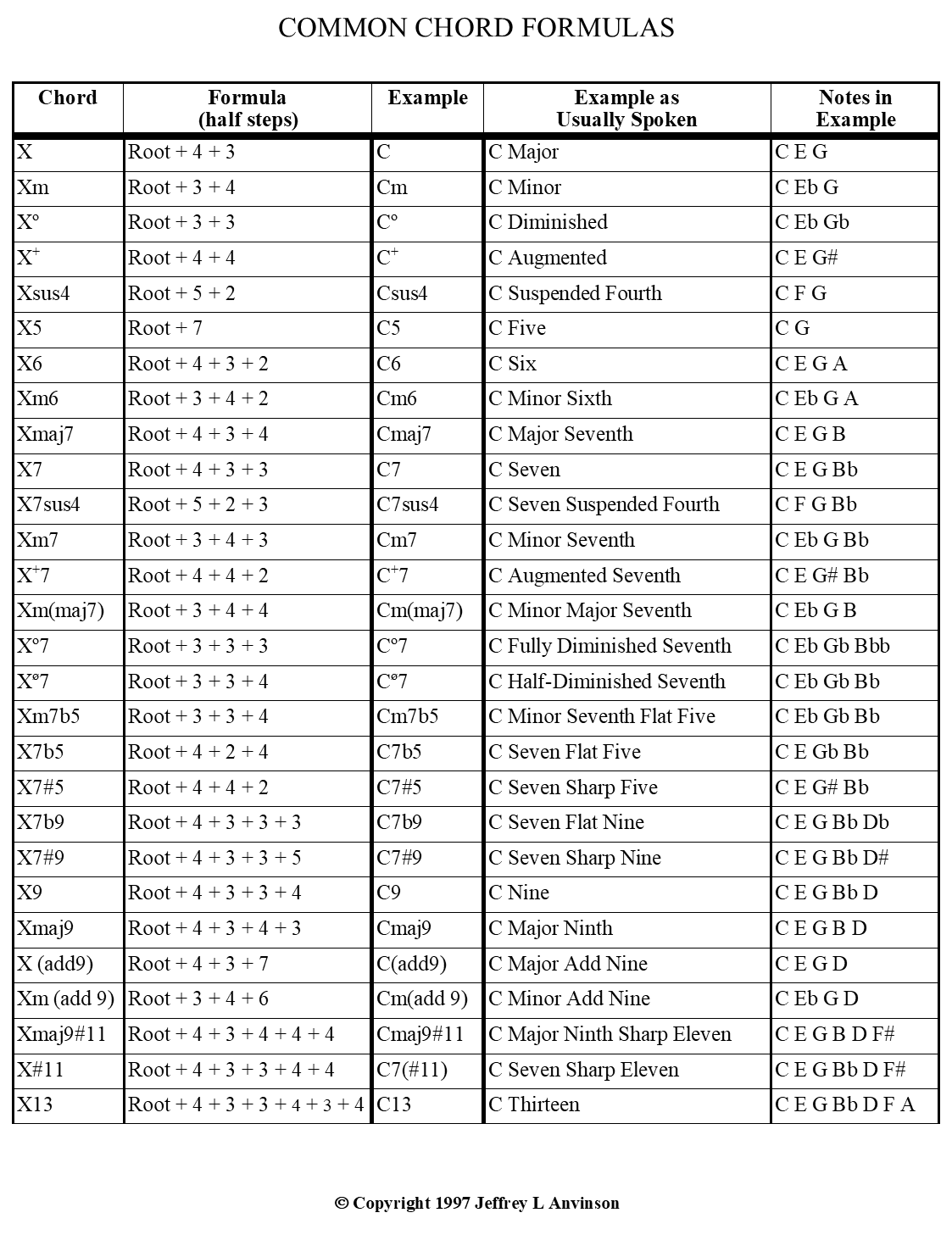
Chord Formulas
an easier way to figure out chord notes (members)
Traditional music theory has a method for constructing chords requiring intervals, scales, scale degree numbers, and other relatively knowledge-based prerequisites. Faced with creating a simpler way to help students construct chords, I came up with this table of common chord formulas.
To use it, start with the root (the pitch of the chord name), and then add notes based on intervals counted in half-steps (abbreviated "HS"). One half-step is the distance between adjacent notes, such as B and C. Remember that when counting half-steps, the first note is not counted, only subsequent ones. This might be compared to how we measure inches, feet, centimeters, or any similar incremental distance.
This table is not exhaustive. There are many other chords not included here, but perhaps at a later date this will be updated to include more.
Here's an example of how to use this table:
Chord: Dm (D minor)
Symbol in Chart: Xm
Root: D
The next note in the chord is D + 3 HS (half-steps): D-0HS, D#-1HS, E-2HS, F-3HS = F
The final note in the chord is F + 4 HS: F-0HS, F#-1HS, G-2HS, G#-3HS, A-4HS = A
The three unique letter names (members) of a Dm chord are D, F, and A.
NOTE: A Dm chord can contain any number of these three members, D, F, and A, arranged in any fashion.
Click here to download a PDF of the following document