My Other Websites
emahle.com  musictheoryetc.com  jeffanvinson.com
letitsnowex.com  uareanangel.com
 

Original music, "You Are an Angel", "Let It Snow (Extravaganza)", and others released on iTunes, Amazon, and elsewhere online.

The Awesome Power of the Circle of Fifths

If you have studied music, you have probably heard of the Circle of Fifths. Although the Circle of Fifths is a little difficult to understand at first, once you get the hang of it, its power will be revealed. It is full of information and mnemonic devices. Pictured below at the end of this article is my particular take on the Circle of Fifths. It adds a few things to the basic circle. (You can download a copy in pdf format using a link below.)

What can it do, this modest one-page document? It is a superhero, with several powers.

• 1. It can leap tall buildings with a single . . . no, that's Superman and Superwoman of course. It can't do that. But it can tell you how many sharps or flats are in each key.
• 2. It can tell you the order in which flats and sharps are added to key signatures.
• 3. It will magically reveal the parallel and relative keys.
• 4. It's color coded cape makes things easier to see than a traditional Circle of Fifths.
• 5. Once you memorize it, you can fold it up into a paper airplane - alas, one without super powers.

Aren't those powers incredible? Let's get started using them. (Put on your super hero cape because some of these concepts can be convoluted.)

Preliminary Instructions

First, you need to know what a fifth is. A fifth is a name for the interval (distance) between two notes that are five letters apart - counted inclusively - in the musical alphabet. As you should know, the musical alphabet is identical to the first seven letters of the complete alphabet: A B C D E F G. So, for example, the note C, and the G directly above C, are a fifth apart because counting from C through G in the musical alphabet will add up to five: C 1, D 2, E 3, F 4, and G 5. We would say that the interval from a C up to the next G, is a fifth. The note G is higher than C. (On a musical staff, the G would be literally higher. It would also sound higher.

Notice in the paragraph above that I was specific about G being "higher" than C. That's important because if you count the distance from C down to G, you will get the number four: C 1, B 2, A 3, G 4. If this seems like sleight of hand, it kind of is. Musical magicians would make a fifth disappear simply by turning it upside down. Presto chango!

Fourths and fifths are much alike, yet they are different. To use the Circle of Fifths we will need to go up a fifth sometimes, and down a fifth other times. Going up will involve alphabetical order, while going down is reverse alphabetical order. We could use fourths instead of fifths, but that's the subject of a possible future article. For now let's just say that fourths are the equivalent of a bad dog (only temporarily, like all the dogs in the world). Fourths - BAD DOG! Fifths - GOOD DOG! No fourths for now, only fifths. (There is nothing wrong with fourths, but for now we'll send them to the kennel.)

If this explanation of a fifth is foggin' up your noggin', then check out the picture and audio file below. (The truth is we can use fourths with the Circle of Fifths, but to make things simpler we'll stick with fifths.)

Now here comes the hard part: Not all fifths are the same. Since the letter names can be raised or lowered using flats or sharps (even the dreadful double flats and sharps), we have different kinds of fifths. For example, a perfect fifth, the kind we need to use with the Circle of Fifths, must be seven half steps apart. If it is six steps apart it is called a diminished fifth, and eight steps, an augmented fifth. We have one good dog and two bad dogs, as the picture below shows. Play the audio clip below the picture to hear how it sounds.

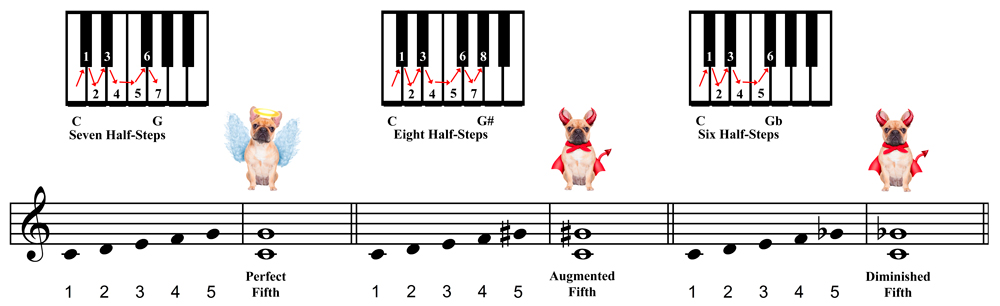
If you're still with me after that difficult discussion of intervals and half-steps, great! The rest of the way should be easier. The point of the top five paragraphs is to impress upon you that we need to use perfect fifths when using the Circle of Fifths for now. (You can use fourths later once you grasp the basic concept.) That's why my particular version of the Circle of Fifths is called the Circle of (Perfect) Fifths. If you use different kinds of fifths, the Circle of Fifths will be rendered useless, a bit like Superman when he encounters Kryptonite.

Music uses two systems of measurement - letter names and half steps. They work together to enable precise measurements. It's like measuring people - we use both height and weight to be more precise.

Super Power Number One: Number of Sharps/Flats in Keys

Let's use the Circle of Fifths to determine the number of sharps or flats there are in different keys. A key is like home base. It's where Superman chills out each day after doing his public service thing. Each key has a certain number of sharps or flats.

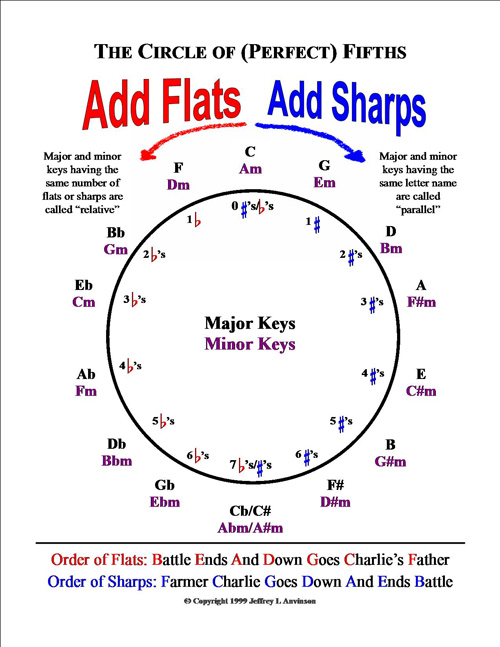
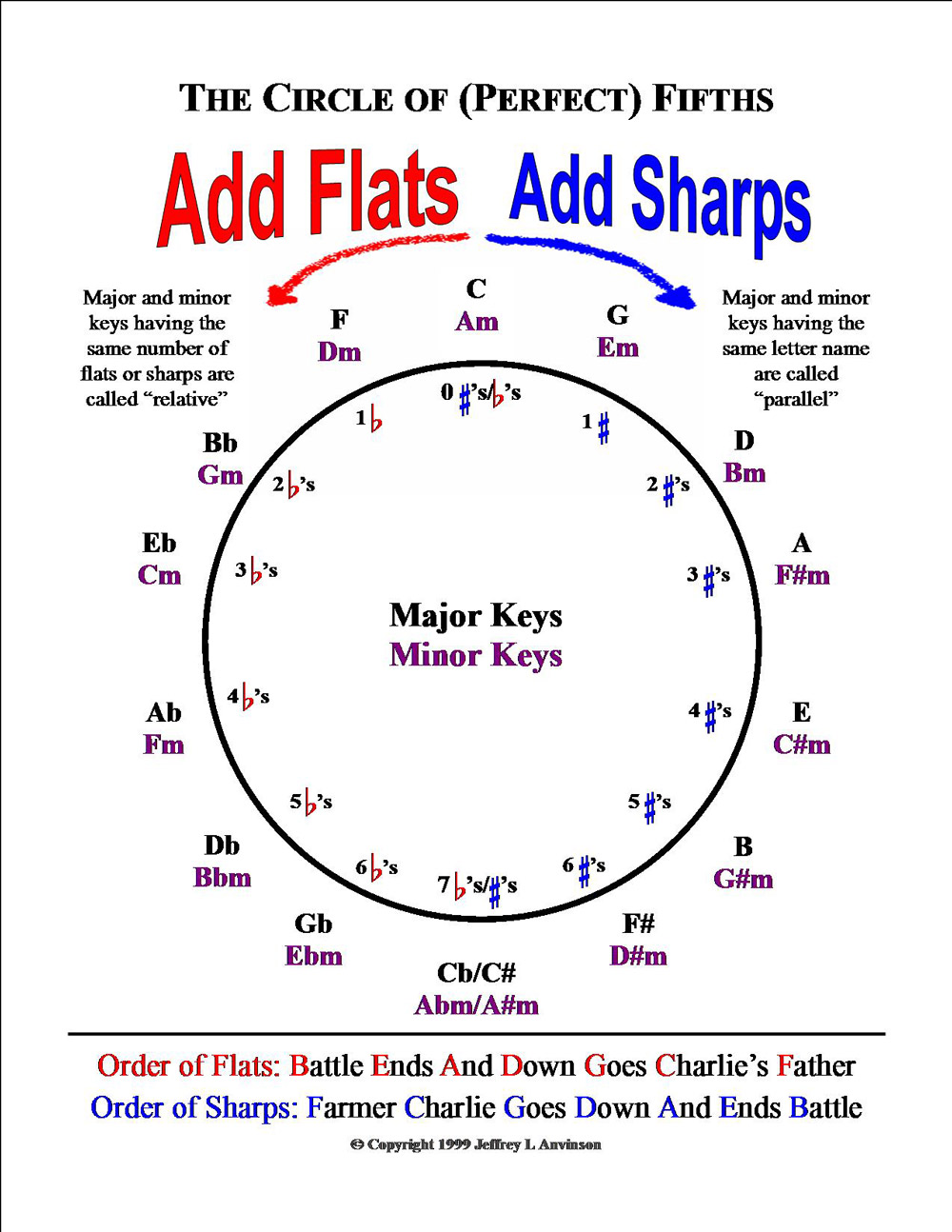
Let's start with the key of C major. Notice on the Circle of Fifths that it has zero sharps and flats. (Don't ask me now why it has zero, though you could click here to find a page on this website that explains it.)

To determine the number of sharps or flats in keys other than c major, we can use perfect fifths. C up a perfect fifth is G, as we discovered above. It turns out that G major uses one sharp. If we go up another perfect fifth we run into D major, which uses two sharps. Then another perfect fifth higher - A major. It has, you guessed it, three sharps. If you look at the Circle of Fifths starting with the C on the top and going clockwise, you will notice that each time you go up another fifth you add another sharp to the key signature.

How about flats? It turns out that if we go down a perfect fifth from C, we get F, which has one flat in its key signature. Go down another perfect fifth to Bb, which has two flats. Another perfect fifth down from Bb to Eb, and we have three flats. On and on, counter clockwise by descending perfect fifths and we get to the last one, Cb, which has seven flats - the most we can reasonably use. (We could keep going down, but we'd get to keys which have eight flats or more, which are considered theoretical keys because there are only seven letters in the alphabet. That's a place we don't want to go. Trust me. It's only trodden by hard core music theorists and composers who want to be rebels.)

Super Power Number Two: Order that Sharps and Flats are Added

The circle of fifths can tell you the order in which sharps and flats are added, but it's confusing and complicated to describe. So, most musicians learn two simple mnemonic phrases instead. They're shown at the bottom of the Circle of Fifths below. Flats and sharps are always added in a specific order. If one sharp is needed, such as the key of G major, F sharp is used. If two sharps are needed you will use the first sharp, F#, and add C sharp. The same method is used in keys that have flats. If you need one flat, it will always be Bb, two flats, Bb and Eb, three flats, Bb, Eb, and Ab, etc. The first letter in each word in the phrase Battle ends and down goes Charlie's father, tells the order in which flats are added: Bb (battle), Eb (ends), Ab (and), etc. The phrase for sharps is Farmer Charlie goes Down And ends battle. If we need one sharp, it will be F# (farmer), two sharps, F# and C# (farmer Charlie), three sharps, F#, C#, and G# (farmer Charlie goes). Nifty huh? Now when you go down clockwise on the right side of the Circle of Fifths you'll notice that G major uses one sharp, F# (farmer), next the key of D major, which uses two sharps, F# and C# (farmer Charlie). You might find all of this complicated at first, but with a little time it will make more sense.

Super Power Number Three: Parallel and Relative Keys

If you want to take a break and grab a soda, please do. We've covered some really complicated territory. When you're ready, come back to learn about the concept of parallel and relative keys.

RELATIVE KEYS    Without getting into too much detail, I'll just start out by saying that for any given number of sharps or flats, two possible keys exist, minor and major. The key of C major has zero flats or sharps and so does the key of A minor. These are called relative keys because they use the same number of sharps or flats. The Circle of Fifths below uses color coding for major and minor keys (black and purple respectively) and relative keys are found side by side. Determining relative keys is a snap with the Circle of Fifths.

PARALLEL KEYS    A major and minor key that have the same letter name (as opposed to the same key signature) are called parallel keys. To determine key signatures for parallel keys we simply look at the Circle of Fifths to tell us the key signature for the major key and then the key signature for the minor key that has the same letter name. For example, the key of C major has zero flats and sharps, while the parallel key of C minor has three flats. It's a little more work than with relative keys, but the Circle of Fifths will let you find them.

Super Power Number Four: Color Coding

Most Circle of Fifths charts are in black and white. The one below is more powerful because it is in color. It is much easier to grasp its concepts with color coding. It's not much of a super power but it is still powerful. (I wouldn't normally use the word "powerful" so much but I'm trying to stick with the theme of this article.)

Conclusion

Well that's it for this web page about the Circle of Fifths. I hope that I was able to show you how useful the Circle of Fifths is. It's one of the many super heroes in music theory.

Jeff Anvinson, owner/operator of JLA Music

(Click here to get a pdf version of the picture shown below. Please don't distribute this pdf by photocopying or posting it on the internet. You may print out one copy for your own use. If you know someone who wants a copy, simply refer them to this website. Please help me protect my intellectual property by respecting my rights.)