My Other Websites
emahle.com  musictheoryetc.com  jeffanvinson.com
letitsnowex.com  uareanangel.com
 

Original music, "You Are an Angel", "Let It Snow (Extravaganza)", and others released on iTunes, Amazon, and elsewhere online.

As any beginner knows, there are two popular systems for learning the scales:

• The CAGED shapes
• The 3-Note-Per-String (3NPS) shapes

There are five scale shapes in all for the CAGED system and seven for the 3NPS system.

In this article, we are not going to concern ourselves with the relative advantages or disadvantages of each of these systems. They do have relative merits, however. For example, the CAGED system explicit introduces the idea of relating scales to chord shapes. The 3NPS system on the other hand has the advantage of yielding consistent picking patterns across strings, hence benefitting speed picking mechanics.

Instead, the aim of this article is simply to provide the beginning guitarist with a simple method for identifying the various scale shapes for each of these systems across the fretboard. For the sake of expositional ease, we will consider the example of the Natural Minor (Aeolian) in the subsequent discussion, but everything that we discuss will be directly applicable with only minor adjustments (and we will detail these adjustments below) to all the modes of the Major.

CAGED System

Let’s start with a discussion of the CAGED system:

• The first thing to note is that the shapes of the CAGED system are built around an underlying infinitely recurring 2 octave pattern. For the case of the Natural Minor, starting from the tonic, the pattern looks like:

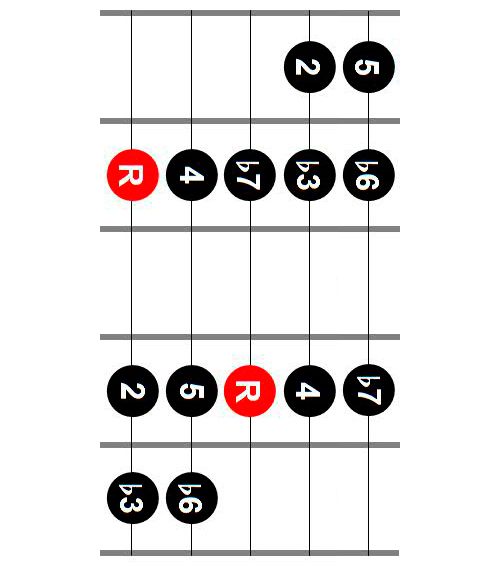
• To build any CAGED shape, first, identify the root note. Then, simply apply the following recurring sequence across the 6 strings (noting that you need to shift up one half-step on the B string). Voila! That’s…it.

As an example, let’s start with a root position on the low E (6th) string. You can see that there are two possible patterns depending on whether you plan to “move up” on the fretboard from the root, or “move down”.

The former delivers what is commonly referred to as the “G” shape in the CAGED system:

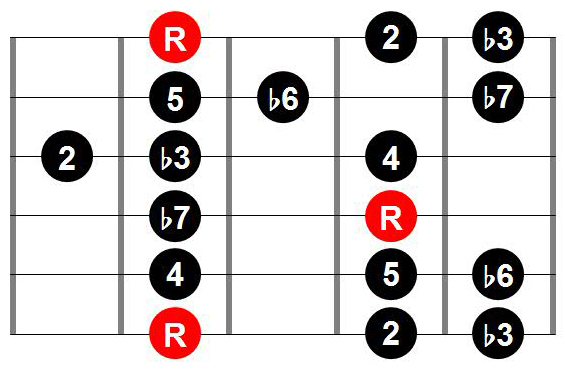
The latter delivers the “A” shape in the CAGED system:

It is important to note that both these shapes are directly obtained from the infinitely recurring 2 octaves pattern above!

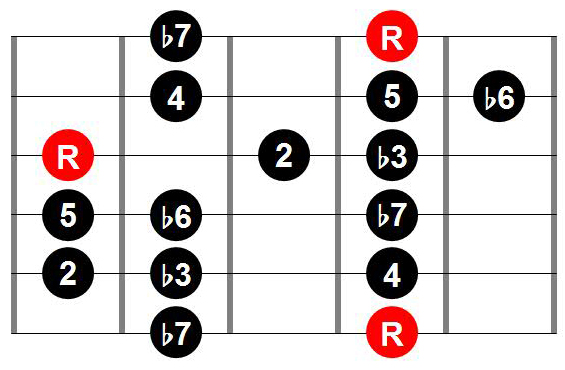
Now, what if we started from a root position on some other string? Let’s just randomly say we wanted to start from a root on the G (3rd) string. And, we wanted to “move up” the fretboard from the root. Well, according to the infinite recurring 2 octave pattern above, that shape, from the G string to the high E string, would look like this (note the half-step shift on the B string):

But, what happens when we “fill-out” the rest of the other 3 strings using the infinitely recurring 2 octave pattern?

That’s right! Turns out, we get the “A” shape!

Hmmm…ok, so, wait a minute, exactly how many unique 6 string patterns can one obtain using the infinitely recurring 2 octave pattern above?

Let’s pin down a root on the 6th string (e.g., A which is on the 5th fret), then, if we move up the frets, we will find that the next root occurs on the 4th string (at the 7th fret), then the 2nd string (on the 10th fret), then the 5th string (on the 12th fret), and finally on the 3rd string (on the 14th fret) before going back to the 6th string again. That is, we have 5 unique roots as we go up the frets before getting back to a root on the starting string; i.e., the 6th string in this example.

Can you see this pattern of root positions in the 5 CAGED shapes?

In terms of the strings, we go through: E-D-B-A-G (and back to E). Note that if there wasn’t the half step shift on the B string, that would be a C there instead of a B, and we would have the letters for CAGED. And, that is why we have 5 CAGED scale shapes. They are obtained by applying the infinite recurring 2 octave pattern above to each of these 5 unique roots across the 6 strings!

That’s it! Therefore, if a guitarist is able to identify all the root positions on the fretboard, and if she is aware of the infinitely recurring 2 octave pattern, then, she can recover any CAGED scale shape within the neighborhood of any root position immediately!

Now, what if we moved away from the Natural Minor to another mode of the Major? It is important to realize that the principles above apply across all the modes of the Major with no loss of generality because the notes for all modes of the Major are exactly the same! Only the root position has changed. To identify the CAGED shapes that apply to any mode of the Major, simply move the root position in the infinite recurring 2 octave pattern and build accordingly. Everything else follows immediately. The end result is the exact same 5 CAGED patterns but with a different arrangement of scale degrees within each shape depending on the mode.

3NPS System

As with the CAGED system, there is an infinitely recurring pattern that underlies the 3NPS scale shapes. The underlying infinitely recurring pattern for the 3 NPS scales (that spans 3 octaves) is:

Note where the root positions are for the Natural Minor in the above infinitely recurring 3 octave pattern. As with the CAGED system, the principles for scale shape building are the same. Identify the root on any string. Then, look at the infinitely recurring pattern above, and “fill-in” the scale shape across all 6 strings (always remembering the shift up one half-step on the B string).

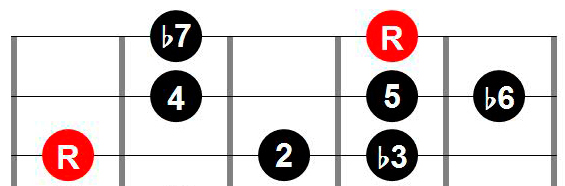
Here is an example with the root on the 6th string:

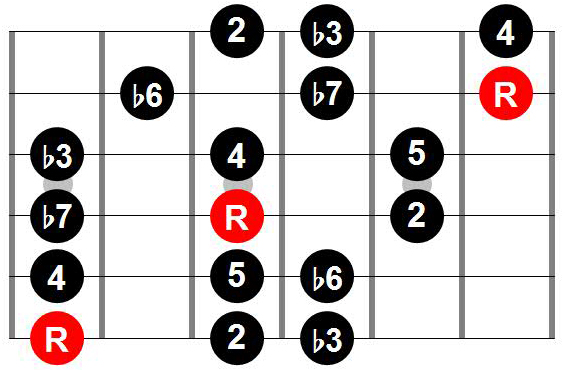
Here is the another 3NPS scale shape with the root on the 6th string:

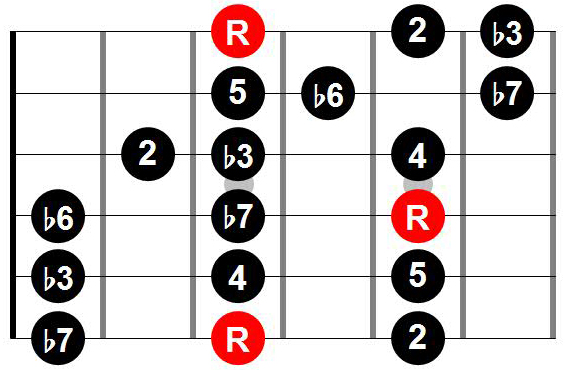
Is there another one? [The answer is yes!]

The 3NPS patterns are best thought of as being based on the diatonic degrees on the low E string. That pattern for the Natural Minor is the well-known: R-W-H-W-W-H-W-(R). Because there are 7 degrees, there will be 7 3NPS scale patterns. You can see this by looking right down across all the scale shapes. Note the starting scale degree for each pattern: they go through b7, R, 2, b3, 4, 5, b6. That is, the diatonic degrees of the Natural Minor! This is interesting for the following reason. First, note that the Natural Minor is a mode of the Major, and therefore all the notes of the Natural Minor are the same notes in the relative Major. Hence, if we start each of the 3NPS shapes in sequence diatonically with notes from that scale (as is done in the pictures), what we have effectively demonstrated is that each of these 3NPS shapes can be thought of as articulating a mode of the Major.

For example, if the 6th string Root ("R") in Shape 2 was A; i.e., we are in the key of A Minor (Aeolian). Then, we know that since A Minor is the relative Minor to C Major, Shape 3 = B Locrian, Shape 4 = C Major, Shape 5 = D Dorian, Shape 6 = E Phrygian, Shape 7 = F Lydian, and Shape 1 = G Mixolydian. We will detail this relationship between the 3NPS shapes and the 7 modes of the Major more thoroughly in another article (The 3-Note-Per-String (3NPS) Scale Shapes and the Modes of the Major Scale).

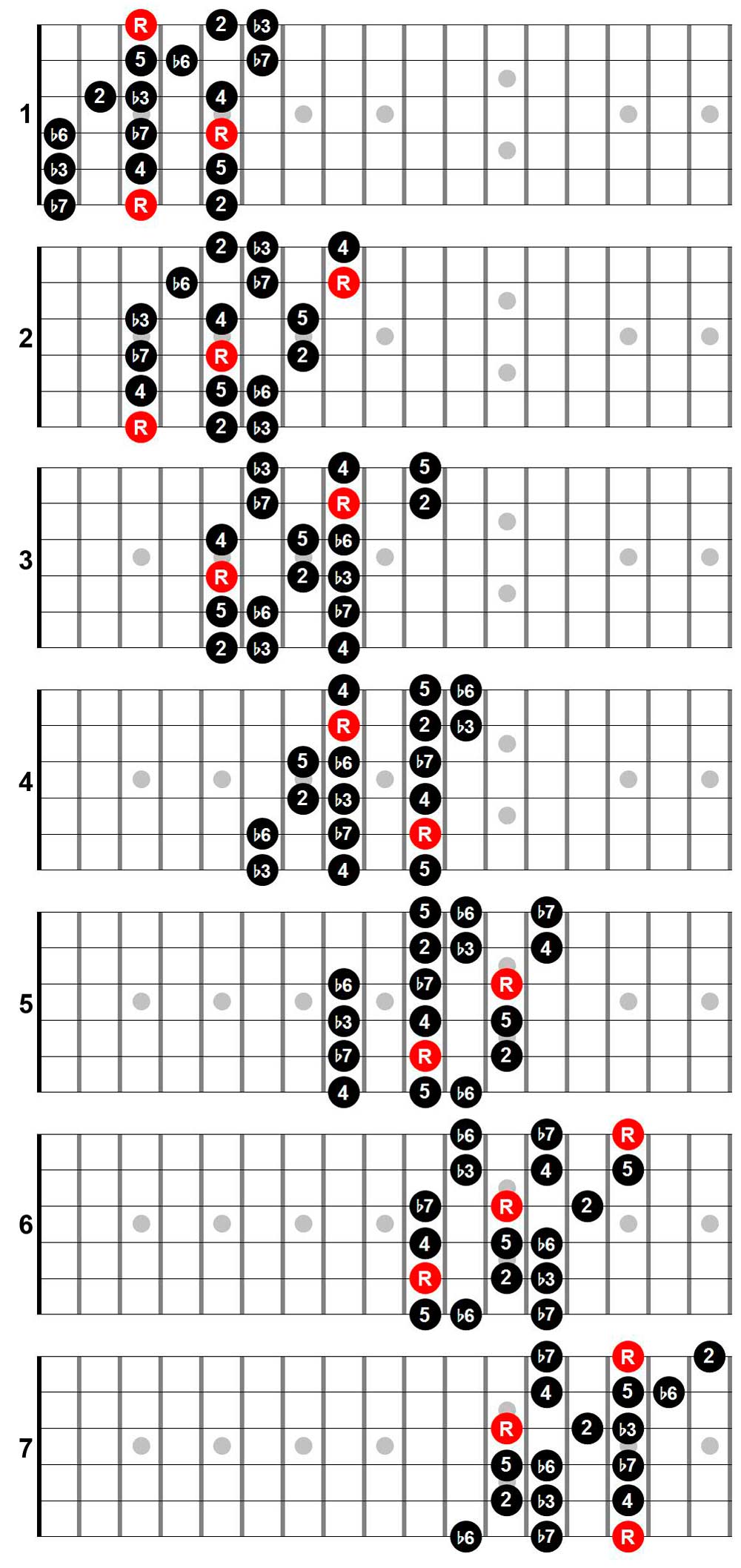
As with the CAGED shapes, the principles above for constructing 3NPS shapes are general to all the modes of the Major. The 7 3NPS shapes will be the same for all modes. However, the pattern of scale degrees within these shapes will be different across modes.